scipy.stats.circvar#
- scipy.stats.circvar(samples, high=6.283185307179586, low=0, axis=None, nan_policy='propagate', *, keepdims=False)[source]#
Compute the circular variance for samples assumed to be in a range.
- Parameters:
- samplesarray_like
Input array.
- highfloat or int, optional
High boundary for the sample range. Default is
2*pi.- lowfloat or int, optional
Low boundary for the sample range. Default is 0.
- axisint or None, default: None
If an int, the axis of the input along which to compute the statistic. The statistic of each axis-slice (e.g. row) of the input will appear in a corresponding element of the output. If
None, the input will be raveled before computing the statistic.- nan_policy{‘propagate’, ‘omit’, ‘raise’}
Defines how to handle input NaNs.
propagate: if a NaN is present in the axis slice (e.g. row) along which the statistic is computed, the corresponding entry of the output will be NaN.omit: NaNs will be omitted when performing the calculation. If insufficient data remains in the axis slice along which the statistic is computed, the corresponding entry of the output will be NaN.raise: if a NaN is present, aValueErrorwill be raised.
- keepdimsbool, default: False
If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the input array.
- Returns:
- circvarfloat
Circular variance.
Notes
This uses the following definition of circular variance:
1-R, whereRis the mean resultant vector. The returned value is in the range [0, 1], 0 standing for no variance, and 1 for a large variance. In the limit of small angles, this value is similar to half the ‘linear’ variance.Beginning in SciPy 1.9,
np.matrixinputs (not recommended for new code) are converted tonp.ndarraybefore the calculation is performed. In this case, the output will be a scalar ornp.ndarrayof appropriate shape rather than a 2Dnp.matrix. Similarly, while masked elements of masked arrays are ignored, the output will be a scalar ornp.ndarrayrather than a masked array withmask=False.References
[1]Fisher, N.I. Statistical analysis of circular data. Cambridge University Press, 1993.
Examples
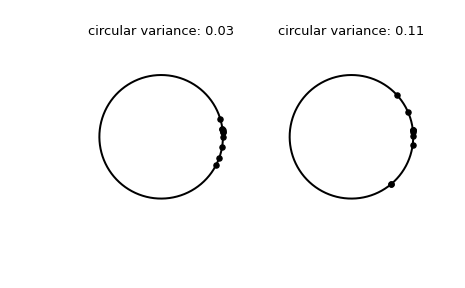
>>> import numpy as np >>> from scipy.stats import circvar >>> import matplotlib.pyplot as plt >>> samples_1 = np.array([0.072, -0.158, 0.077, 0.108, 0.286, ... 0.133, -0.473, -0.001, -0.348, 0.131]) >>> samples_2 = np.array([0.111, -0.879, 0.078, 0.733, 0.421, ... 0.104, -0.136, -0.867, 0.012, 0.105]) >>> circvar_1 = circvar(samples_1) >>> circvar_2 = circvar(samples_2)
Plot the samples.
>>> fig, (left, right) = plt.subplots(ncols=2) >>> for image in (left, right): ... image.plot(np.cos(np.linspace(0, 2*np.pi, 500)), ... np.sin(np.linspace(0, 2*np.pi, 500)), ... c='k') ... image.axis('equal') ... image.axis('off') >>> left.scatter(np.cos(samples_1), np.sin(samples_1), c='k', s=15) >>> left.set_title(f"circular variance: {np.round(circvar_1, 2)!r}") >>> right.scatter(np.cos(samples_2), np.sin(samples_2), c='k', s=15) >>> right.set_title(f"circular variance: {np.round(circvar_2, 2)!r}") >>> plt.show()