scipy.spatial.HalfspaceIntersection#

class scipy.spatial.HalfspaceIntersection(halfspaces, interior_point, incremental=False, qhull_options=None)#

Halfspace intersections in N dimensions.

New in version 0.19.0.

Parameters:

halfspacesndarray of floats, shape (nineq, ndim+1): Stacked Inequalities of the form Ax + b <= 0 in format [A; b]
interior_pointndarray of floats, shape (ndim,): Point clearly inside the region defined by halfspaces. Also called a feasible point, it can be obtained by linear programming.
incrementalbool, optional: Allow adding new halfspaces incrementally. This takes up some additional resources.
qhull_optionsstr, optional: Additional options to pass to Qhull. See Qhull manual for details. (Default: “Qx” for ndim > 4 and “” otherwise) Option “H” is always enabled.

Raises:

QhullError: Raised when Qhull encounters an error condition, such as geometrical degeneracy when options to resolve are not enabled.
ValueError: Raised if an incompatible array is given as input.

Notes

The intersections are computed using the Qhull library. This reproduces the “qhalf” functionality of Qhull.

References

[Qhull]

http://www.qhull.org/

[1]

S. Boyd, L. Vandenberghe, Convex Optimization, available at http://stanford.edu/~boyd/cvxbook/

Examples

Halfspace intersection of planes forming some polygon

>>> from scipy.spatial import HalfspaceIntersection
>>> import numpy as np
>>> halfspaces = np.array([[-1, 0., 0.],
...                        [0., -1., 0.],
...                        [2., 1., -4.],
...                        [-0.5, 1., -2.]])
>>> feasible_point = np.array([0.5, 0.5])
>>> hs = HalfspaceIntersection(halfspaces, feasible_point)

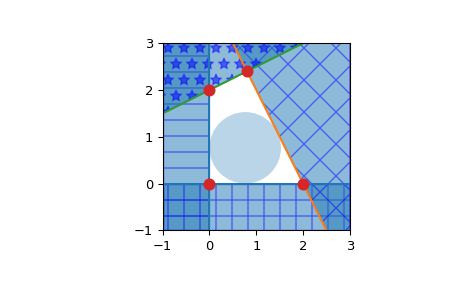
Plot halfspaces as filled regions and intersection points:

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(1, 1, 1, aspect='equal')
>>> xlim, ylim = (-1, 3), (-1, 3)
>>> ax.set_xlim(xlim)
>>> ax.set_ylim(ylim)
>>> x = np.linspace(-1, 3, 100)
>>> symbols = ['-', '+', 'x', '*']
>>> signs = [0, 0, -1, -1]
>>> fmt = {"color": None, "edgecolor": "b", "alpha": 0.5}
>>> for h, sym, sign in zip(halfspaces, symbols, signs):
...     hlist = h.tolist()
...     fmt["hatch"] = sym
...     if h[1]== 0:
...         ax.axvline(-h[2]/h[0], label='{}x+{}y+{}=0'.format(*hlist))
...         xi = np.linspace(xlim[sign], -h[2]/h[0], 100)
...         ax.fill_between(xi, ylim[0], ylim[1], **fmt)
...     else:
...         ax.plot(x, (-h[2]-h[0]*x)/h[1], label='{}x+{}y+{}=0'.format(*hlist))
...         ax.fill_between(x, (-h[2]-h[0]*x)/h[1], ylim[sign], **fmt)
>>> x, y = zip(*hs.intersections)
>>> ax.plot(x, y, 'o', markersize=8)

By default, qhull does not provide with a way to compute an interior point. This can easily be computed using linear programming. Considering halfspaces of the form \(Ax + b \leq 0\), solving the linear program:

\[ \begin{align}\begin{aligned}max \: y\\s.t. Ax + y ||A_i|| \leq -b\end{aligned}\end{align} \]

With \(A_i\) being the rows of A, i.e. the normals to each plane.

Will yield a point x that is furthest inside the convex polyhedron. To be precise, it is the center of the largest hypersphere of radius y inscribed in the polyhedron. This point is called the Chebyshev center of the polyhedron (see [1] 4.3.1, pp148-149). The equations outputted by Qhull are always normalized.

>>> from scipy.optimize import linprog
>>> from matplotlib.patches import Circle
>>> norm_vector = np.reshape(np.linalg.norm(halfspaces[:, :-1], axis=1),
...     (halfspaces.shape[0], 1))
>>> c = np.zeros((halfspaces.shape[1],))
>>> c[-1] = -1
>>> A = np.hstack((halfspaces[:, :-1], norm_vector))
>>> b = - halfspaces[:, -1:]
>>> res = linprog(c, A_ub=A, b_ub=b, bounds=(None, None))
>>> x = res.x[:-1]
>>> y = res.x[-1]
>>> circle = Circle(x, radius=y, alpha=0.3)
>>> ax.add_patch(circle)
>>> plt.legend(bbox_to_anchor=(1.6, 1.0))
>>> plt.show()

../../_images/scipy-spatial-HalfspaceIntersection-1.png

Attributes:

halfspacesndarray of double, shape (nineq, ndim+1): Input halfspaces.
interior_point :ndarray of floats, shape (ndim,): Input interior point.
intersectionsndarray of double, shape (ninter, ndim): Intersections of all halfspaces.
dual_pointsndarray of double, shape (nineq, ndim): Dual points of the input halfspaces.
dual_facetslist of lists of ints: Indices of points forming the (non necessarily simplicial) facets of the dual convex hull.
dual_verticesndarray of ints, shape (nvertices,): Indices of halfspaces forming the vertices of the dual convex hull. For 2-D convex hulls, the vertices are in counterclockwise order. For other dimensions, they are in input order.
dual_equationsndarray of double, shape (nfacet, ndim+1): [normal, offset] forming the hyperplane equation of the dual facet (see Qhull documentation for more).
dual_areafloat: Area of the dual convex hull
dual_volumefloat: Volume of the dual convex hull

Methods

`add_halfspaces`(halfspaces[, restart])	Process a set of additional new halfspaces.
`close`()	Finish incremental processing.