scipy.signal.chirp

scipy.signal.chirp(t, f0, t1, f1, method='linear', phi=0, vertex_zero=True)

Frequency-swept cosine generator.

In the following, ‘Hz’ should be interpreted as ‘cycles per unit’; there is no requirement here that the unit is one second. The important distinction is that the units of rotation are cycles, not radians. Likewise, t could be a measurement of space instead of time.

Parameters:

tarray_like

Times at which to evaluate the waveform.

f0float

Frequency (e.g. Hz) at time t=0.

t1float

Time at which f1 is specified.

f1float

Frequency (e.g. Hz) of the waveform at time t1.

method{‘linear’, ‘quadratic’, ‘logarithmic’, ‘hyperbolic’}, optional

Kind of frequency sweep. If not given, linear is assumed. See Notes below for more details.

phifloat, optional

Phase offset, in degrees. Default is 0.

vertex_zerobool, optional

This parameter is only used when method is ‘quadratic’. It determines whether the vertex of the parabola that is the graph of the frequency is at t=0 or t=t1.

Returns:

yndarray

A numpy array containing the signal evaluated at t with the requested time-varying frequency. More precisely, the function returns cos(phase + (pi/180)*phi) where phase is the integral (from 0 to t) of 2*pi*f(t). f(t) is defined below.

See also

sweep_poly

Notes

There are four options for the method. The following formulas give the instantaneous frequency (in Hz) of the signal generated by chirp(). For convenience, the shorter names shown below may also be used.

linear, lin, li:

f(t) = f0 + (f1 - f0) * t / t1

quadratic, quad, q:

The graph of the frequency f(t) is a parabola through (0, f0) and (t1, f1). By default, the vertex of the parabola is at (0, f0). If vertex_zero is False, then the vertex is at (t1, f1). The formula is:

if vertex_zero is True:

f(t) = f0 + (f1 - f0) * t**2 / t1**2

else:

f(t) = f1 - (f1 - f0) * (t1 - t)**2 / t1**2

To use a more general quadratic function, or an arbitrary polynomial, use the function scipy.signal.sweep_poly.

logarithmic, log, lo:

f(t) = f0 * (f1/f0)**(t/t1)

f0 and f1 must be nonzero and have the same sign.

This signal is also known as a geometric or exponential chirp.

hyperbolic, hyp:

f(t) = f0*f1*t1 / ((f0 - f1)*t + f1*t1)

f0 and f1 must be nonzero.

Examples

Try it in your browser!

The following will be used in the examples:

>>> import numpy as np
>>> from scipy.signal import chirp, spectrogram
>>> import matplotlib.pyplot as plt

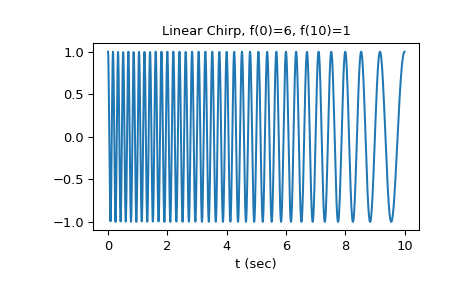
For the first example, we’ll plot the waveform for a linear chirp from 6 Hz to 1 Hz over 10 seconds:

>>> t = np.linspace(0, 10, 1500)
>>> w = chirp(t, f0=6, f1=1, t1=10, method='linear')
>>> plt.plot(t, w)
>>> plt.title("Linear Chirp, f(0)=6, f(10)=1")
>>> plt.xlabel('t (sec)')
>>> plt.show()

For the remaining examples, we’ll use higher frequency ranges, and demonstrate the result using scipy.signal.spectrogram. We’ll use a 4 second interval sampled at 7200 Hz.

>>> fs = 7200
>>> T = 4
>>> t = np.arange(0, int(T*fs)) / fs

We’ll use this function to plot the spectrogram in each example.

>>> def plot_spectrogram(title, w, fs):
...     ff, tt, Sxx = spectrogram(w, fs=fs, nperseg=256, nfft=576)
...     fig, ax = plt.subplots()
...     ax.pcolormesh(tt, ff[:145], Sxx[:145], cmap='gray_r',
...                   shading='gouraud')
...     ax.set_title(title)
...     ax.set_xlabel('t (sec)')
...     ax.set_ylabel('Frequency (Hz)')
...     ax.grid(True)
...

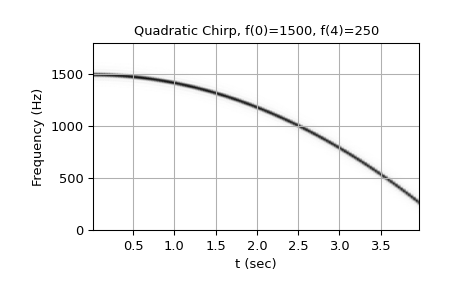
Quadratic chirp from 1500 Hz to 250 Hz (vertex of the parabolic curve of the frequency is at t=0):

>>> w = chirp(t, f0=1500, f1=250, t1=T, method='quadratic')
>>> plot_spectrogram(f'Quadratic Chirp, f(0)=1500, f({T})=250', w, fs)
>>> plt.show()

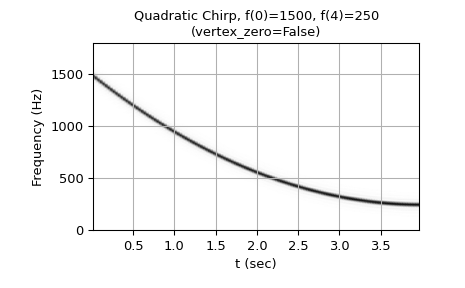
Quadratic chirp from 1500 Hz to 250 Hz (vertex of the parabolic curve of the frequency is at t=T):

>>> w = chirp(t, f0=1500, f1=250, t1=T, method='quadratic',
...           vertex_zero=False)
>>> plot_spectrogram(f'Quadratic Chirp, f(0)=1500, f({T})=250\n' +
...                  '(vertex_zero=False)', w, fs)
>>> plt.show()

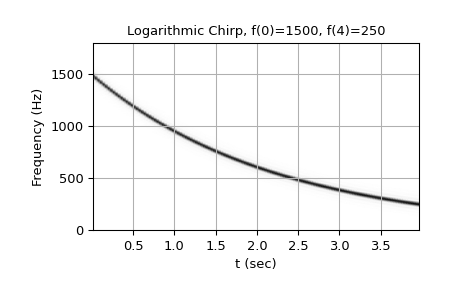
Logarithmic chirp from 1500 Hz to 250 Hz:

>>> w = chirp(t, f0=1500, f1=250, t1=T, method='logarithmic')
>>> plot_spectrogram(f'Logarithmic Chirp, f(0)=1500, f({T})=250', w, fs)
>>> plt.show()

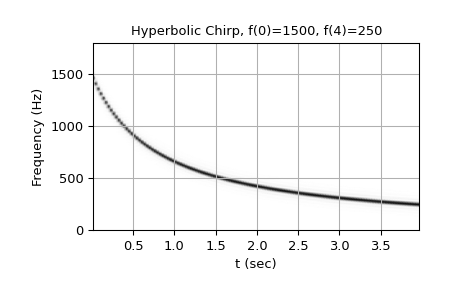
Hyperbolic chirp from 1500 Hz to 250 Hz:

>>> w = chirp(t, f0=1500, f1=250, t1=T, method='hyperbolic')
>>> plot_spectrogram(f'Hyperbolic Chirp, f(0)=1500, f({T})=250', w, fs)
>>> plt.show()

Go BackOpen In Tab