scipy.signal.ShortTimeFFT.from_dual

classmethod ShortTimeFFT.from_dual(dual_win, hop, fs, *, fft_mode='onesided', mfft=None, scale_to=None, phase_shift=0)

Instantiate a ShortTimeFFT by only providing a dual window.

If an STFT is invertible, it is possible to calculate the window win from a given dual window dual_win. All other parameters have the same meaning as in the initializer of ShortTimeFFT.

As explained in the Short-Time Fourier Transform section of the SciPy User Guide, an invertible STFT can be interpreted as series expansion of time-shifted and frequency modulated dual windows. E.g., the series coefficient S[q,p] belongs to the term, which shifted dual_win by p * delta_t and multiplied it by exp( 2 * j * pi * t * q * delta_f).

See also

from_window

Create instance by wrapping get_window.

ShortTimeFFT

Create instance using standard initializer.

Examples

Try it in your browser!

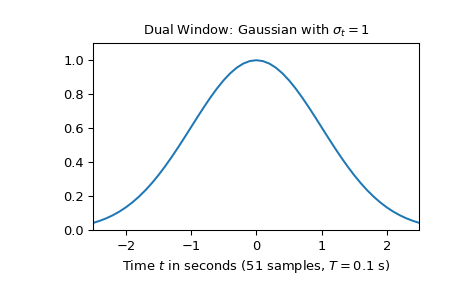
The following example discusses decomposing a signal into time- and frequency-shifted Gaussians. A Gaussian with standard deviation of one made up of 51 samples will be used:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import ShortTimeFFT
>>> from scipy.signal.windows import gaussian
...
>>> T, N = 0.1, 51
>>> d_win = gaussian(N, std=1/T, sym=True)  # symmetric Gaussian window
>>> t = T * (np.arange(N) - N//2)
...
>>> fg1, ax1 = plt.subplots()
>>> ax1.set_title(r"Dual Window: Gaussian with $\sigma_t=1$")
>>> ax1.set(xlabel=f"Time $t$ in seconds ({N} samples, $T={T}$ s)",
...        xlim=(t[0], t[-1]), ylim=(0, 1.1*max(d_win)))
>>> ax1.plot(t, d_win, 'C0-')

The following plot with the overlap of 41, 11 and 2 samples show how the hop interval affects the shape of the window win:

>>> fig2, axx = plt.subplots(3, 1, sharex='all')
...
>>> axx[0].set_title(r"Windows for hop$\in\{10, 40, 49\}$")
>>> for c_, h_ in enumerate([10, 40, 49]):
...     SFT = ShortTimeFFT.from_dual(d_win, h_, 1/T)
...     axx[c_].plot(t + h_ * T, SFT.win, 'k--', alpha=.3, label=None)
...     axx[c_].plot(t - h_ * T, SFT.win, 'k:', alpha=.3, label=None)
...     axx[c_].plot(t, SFT.win, f'C{c_+1}',
...                     label=r"$\Delta t=%0.1f\,$s" % SFT.delta_t)
...     axx[c_].set_ylim(0, 1.1*max(SFT.win))
...     axx[c_].legend(loc='center')
>>> axx[-1].set(xlabel=f"Time $t$ in seconds ({N} samples, $T={T}$ s)",
...             xlim=(t[0], t[-1]))
>>> plt.show()

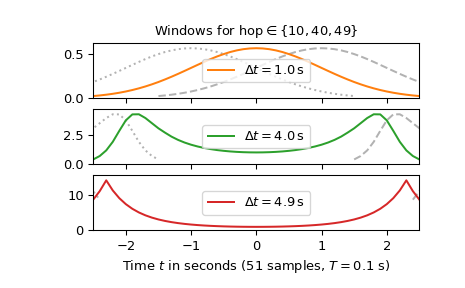
Beside the window win centered at t = 0 the previous (t = -delta_t) and following window (t = delta_t) are depicted. It can be seen that for small hop intervals, the window is compact and smooth, having a good time-frequency concentration in the STFT. For the large hop interval of 4.9 s, the window has small values around t = 0, which are not covered by the overlap of the adjacent windows, which could lead to numeric inaccuracies. Furthermore, the peaky shape at the beginning and the end of the window points to a higher bandwidth, resulting in a poorer time-frequency resolution of the STFT. Hence, the choice of the hop interval will be a compromise between a time-frequency resolution and memory requirements demanded by small hop sizes.

Go BackOpen In Tab