Ctrl+K

scipy.interpolate.LinearNDInterpolator#

class scipy.interpolate.LinearNDInterpolator(points, values, fill_value=np.nan, rescale=False)#

Piecewise linear interpolator in N > 1 dimensions.

New in version 0.9.

Parameters:
pointsndarray of floats, shape (npoints, ndims); or Delaunay

2-D array of data point coordinates, or a precomputed Delaunay triangulation.

valuesndarray of float or complex, shape (npoints, …), optional

N-D array of data values at points. The length of values along the first axis must be equal to the length of points. Unlike some interpolators, the interpolation axis cannot be changed.

fill_valuefloat, optional

Value used to fill in for requested points outside of the convex hull of the input points. If not provided, then the default is nan.

rescalebool, optional

Rescale points to unit cube before performing interpolation. This is useful if some of the input dimensions have incommensurable units and differ by many orders of magnitude.

See also

griddata

Interpolate unstructured D-D data.

NearestNDInterpolator

Nearest-neighbor interpolator in N dimensions.

CloughTocher2DInterpolator

Piecewise cubic, C1 smooth, curvature-minimizing interpolator in 2D.

interpn

Interpolation on a regular grid or rectilinear grid.

RegularGridInterpolator

Interpolator on a regular or rectilinear grid in arbitrary dimensions (interpn wraps this class).

Notes

The interpolant is constructed by triangulating the input data with Qhull [1], and on each triangle performing linear barycentric interpolation.

Note

For data on a regular grid use interpn instead.

References

Examples

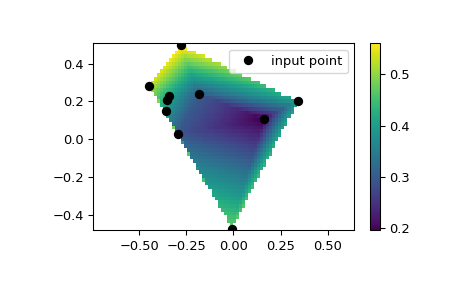
We can interpolate values on a 2D plane:

>>> from scipy.interpolate import LinearNDInterpolator
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> x = rng.random(10) - 0.5
>>> y = rng.random(10) - 0.5
>>> z = np.hypot(x, y)
>>> X = np.linspace(min(x), max(x))
>>> Y = np.linspace(min(y), max(y))
>>> X, Y = np.meshgrid(X, Y)  # 2D grid for interpolation
>>> interp = LinearNDInterpolator(list(zip(x, y)), z)
>>> Z = interp(X, Y)
>>> plt.pcolormesh(X, Y, Z, shading='auto')
>>> plt.plot(x, y, "ok", label="input point")
>>> plt.legend()
>>> plt.colorbar()
>>> plt.axis("equal")
>>> plt.show()
../../_images/scipy-interpolate-LinearNDInterpolator-1.png

Methods

__call__(xi)

Evaluate interpolator at given points.
On this page