scipy.cluster.vq.kmeans2

scipy.cluster.vq.kmeans2(data, k, iter=10, thresh=1e-05, minit='random', missing='warn', check_finite=True, *, seed=None)

Classify a set of observations into k clusters using the k-means algorithm.

The algorithm attempts to minimize the Euclidean distance between observations and centroids. Several initialization methods are included.

Parameters:

datandarray

A ‘M’ by ‘N’ array of ‘M’ observations in ‘N’ dimensions or a length ‘M’ array of ‘M’ 1-D observations.

kint or ndarray

The number of clusters to form as well as the number of centroids to generate. If minit initialization string is ‘matrix’, or if a ndarray is given instead, it is interpreted as initial cluster to use instead.

iterint, optional

Number of iterations of the k-means algorithm to run. Note that this differs in meaning from the iters parameter to the kmeans function.

threshfloat, optional

(not used yet)

minitstr, optional

Method for initialization. Available methods are ‘random’, ‘points’, ‘++’ and ‘matrix’:

‘random’: generate k centroids from a Gaussian with mean and variance estimated from the data.

‘points’: choose k observations (rows) at random from data for the initial centroids.

‘++’: choose k observations accordingly to the kmeans++ method (careful seeding)

‘matrix’: interpret the k parameter as a k by M (or length k array for 1-D data) array of initial centroids.

missingstr, optional

Method to deal with empty clusters. Available methods are ‘warn’ and ‘raise’:

‘warn’: give a warning and continue.

‘raise’: raise an ClusterError and terminate the algorithm.

check_finitebool, optional

Whether to check that the input matrices contain only finite numbers. Disabling may give a performance gain, but may result in problems (crashes, non-termination) if the inputs do contain infinities or NaNs. Default: True

seed{None, int, numpy.random.Generator, numpy.random.RandomState}, optional

Seed for initializing the pseudo-random number generator. If seed is None (or numpy.random), the numpy.random.RandomState singleton is used. If seed is an int, a new RandomState instance is used, seeded with seed. If seed is already a Generator or RandomState instance then that instance is used. The default is None.

Returns:

centroidndarray

A ‘k’ by ‘N’ array of centroids found at the last iteration of k-means.

labelndarray

label[i] is the code or index of the centroid the ith observation is closest to.

See also

kmeans

References

[1]

D. Arthur and S. Vassilvitskii, “k-means++: the advantages of careful seeding”, Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, 2007.

Examples

Try it in your browser!

>>> from scipy.cluster.vq import kmeans2
>>> import matplotlib.pyplot as plt
>>> import numpy as np

Create z, an array with shape (100, 2) containing a mixture of samples from three multivariate normal distributions.

>>> rng = np.random.default_rng()
>>> a = rng.multivariate_normal([0, 6], [[2, 1], [1, 1.5]], size=45)
>>> b = rng.multivariate_normal([2, 0], [[1, -1], [-1, 3]], size=30)
>>> c = rng.multivariate_normal([6, 4], [[5, 0], [0, 1.2]], size=25)
>>> z = np.concatenate((a, b, c))
>>> rng.shuffle(z)

Compute three clusters.

>>> centroid, label = kmeans2(z, 3, minit='points')
>>> centroid
array([[ 2.22274463, -0.61666946],  # may vary
       [ 0.54069047,  5.86541444],
       [ 6.73846769,  4.01991898]])

How many points are in each cluster?

>>> counts = np.bincount(label)
>>> counts
array([29, 51, 20])  # may vary

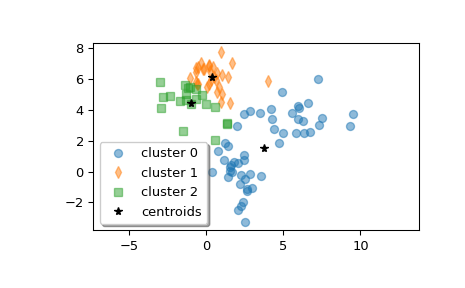
Plot the clusters.

>>> w0 = z[label == 0]
>>> w1 = z[label == 1]
>>> w2 = z[label == 2]
>>> plt.plot(w0[:, 0], w0[:, 1], 'o', alpha=0.5, label='cluster 0')
>>> plt.plot(w1[:, 0], w1[:, 1], 'd', alpha=0.5, label='cluster 1')
>>> plt.plot(w2[:, 0], w2[:, 1], 's', alpha=0.5, label='cluster 2')
>>> plt.plot(centroid[:, 0], centroid[:, 1], 'k*', label='centroids')
>>> plt.axis('equal')
>>> plt.legend(shadow=True)
>>> plt.show()

Go BackOpen In Tab